Visualising π
Visualising the first 1000 and 10000 digits of π, to see if there are any interesting patterns to see.
Ensuring that π is accurate
Python’s math.pi is only so precise, π rounded to a 15 decimal places in a float datatype.
Therefore we need another source for the digits. My solution it to just retrieve it from the internet, as this does not require implementing my own algorithm.
First we need to get first 10000 digits (from a dataset on https://www.joyofpi.com/pi.html), however we will only be using the first 1000 for this visualisation.
with open('data/pi_10000.txt','r') as infile:
digit_str = next(infile)
print(len(digit_str))
print('3.' + digit_str[:50] + '...')
10000
3.14159265358979323846264338327950288419716939937510...
Goal of the Visualisation
How does the average value of π change over the first 1000 digits?
To visualise this, we need to find the average value of π up to the nth digit, for 1<=n<=1000
An efficient method is by calculating the cumulative average, based on:
- the last average
- the N values counted so far
- the n+1 th value
# show change in average of digit over 'time'
def iterate_pi_digits(digit_str):
"""generator function that yields each decimal from the file as an integer
"""
for ch in digit_str:
yield int(ch)
def cumulative_avg(value, last_avg, N):
"""cumulative average
based off of the formula found here:
http://www.iitk.ac.in/esc101/08Jan/lecnotes/lecture22.pdf
Avg(N) = (Avg(N-1) * (N-1)+ Nth element ) / N
"""
return (last_avg * (N-1) + value) / N
from itertools import islice
def gen_plot_features(n_total_digits=100):
"""generator function that yields the cumulative averages
up to the value of n_total_digits.
return the nth digit, the value of n, and the nth cumulative average
"""
last_avg = 1
N = 1
for value in islice(iterate_pi_digits(digit_str), n_total_digits):
last_avg = cumulative_avg(value,last_avg, N)
yield value, N, last_avg
N += 1
import matplotlib.pyplot as plt
import seaborn as sns
% matplotlib inline
sns.set_style("whitegrid")
# using 1000 digits of π for this visualisation
n_total_digits = 1000
digits, x, y = zip(*gen_plot_features(n_total_digits))
fig, ax = plt.subplots(figsize=(14,7))
# plots
ax.plot(x,digits,'.', color='#2F9FBF') # value at nth decimal place
ax.plot(x,y,color='#003242') # cumulative average at nth decimal place
# descriptions
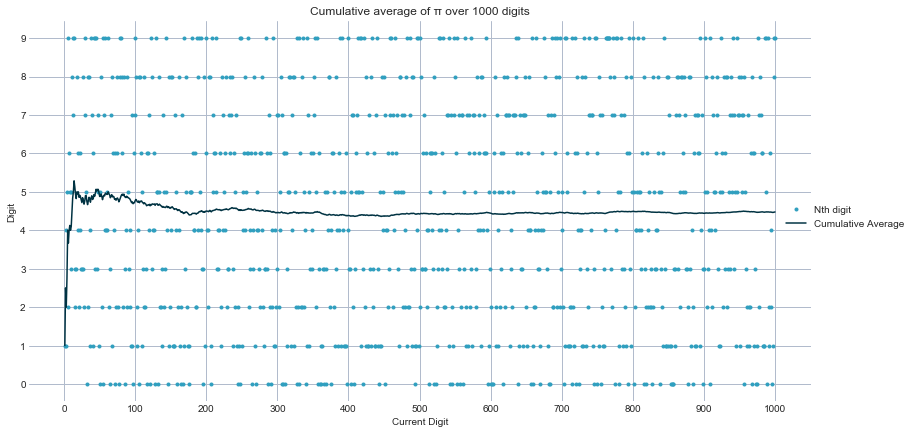
ax.set_title(f"Cumulative average of π over {n_total_digits} digits")
ax.set_xlabel("Current Digit")
ax.set_ylabel("Digit")
# change number of bins for x and y axes
ax.locator_params(axis='y', nbins=10)
ax.locator_params(axis='x', nbins=20)
# add grid
ax.grid(color="#b1bbcc", linestyle='-', linewidth=1)
# remove plot edges
sns.despine(fig, left=True, bottom=True)
# add legend
fig.legend(['Nth digit','Cumulative Average'], loc=5)

Observations
- the value for the cumulative average is unstable until n > ~200, then appears to stabilise at 4.5.
- The digit values appear to have positive linear stripes across them. This could be another point to visualise.
Feedback on the graph
From the post i submitted on this reddit post
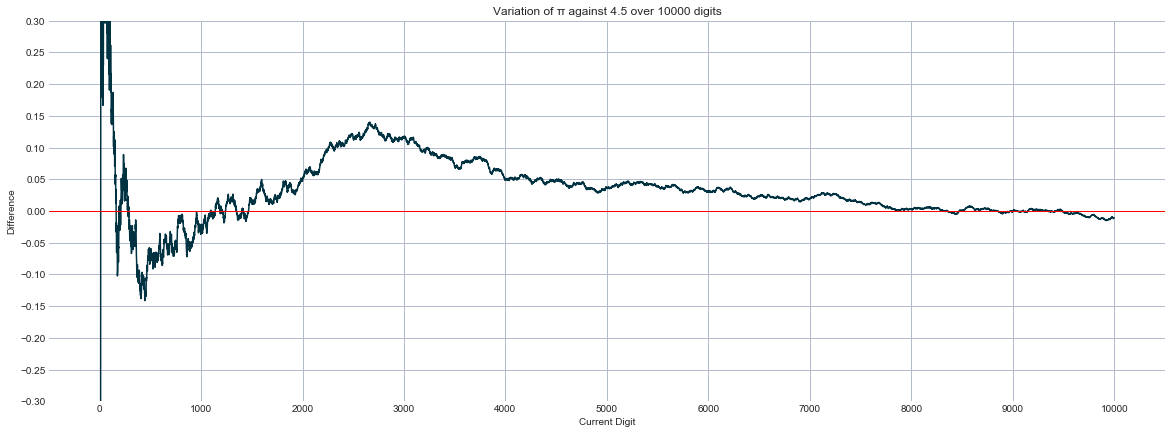
It was noted that the values seem to approach 4.5 (“never asymptote to 4.5”). To check this, i used a spectrogram (line graph showing variation around a point over the x dimension) I used 10000 digits of π to see if the cumulative average approaches 4.5, and if it crosses the threshold.
def diff_to_const(const,arr):
""" compare the values of an array to a constant value
"""
for ele in arr:
yield ele - const
n_total_digits = 10000
digits, x, y = zip(*gen_plot_features(n_total_digits))
fig, ax = plt.subplots(figsize=(20,7))
# plots
ax.plot(x,list(diff_to_const(4.5,y)), color='#003242')
ax.axhline(linewidth=1, color='r')
# descriptions
ax.set_title(f"Variation of π against 4.5 over {n_total_digits} digits")
ax.set_xlabel("Current Digit")
ax.set_ylabel("Difference")
# change number of bins for x and y axes
ax.locator_params(axis='y', nbins=20)
ax.locator_params(axis='x', nbins=20)
ax.grid(color="#b1bbcc", linestyle='-', linewidth=1)
# remove plot edges
sns.despine(fig, left=True, bottom=True)
ax.set_ylim(-0.3,0.3)
# add legend
#fig.legend(['Nth digit','Cumulative Average'], loc=5)
for i in range(7000,10000):
if y[i] < 4.5:
print(i)
break
7882
We can see that the cumulative average digit value for π exceeds 4.5 until ~7800. This is anecdotal evidence of a convergence of average digit values to 4.5.
However, I could not conclude this to be a comprensive proof, due to how few digits of π are used here.